Matemático cria método que ajuda no aprendizado de equação de 1º grau

O presente artigo sugere uma proposta criativa e significativa, no ensino e aprendizagem de equação de 1º grau, e expressões numéricas com o uso da Modelagem Matemática e sua aplicação na vida real, para isso utilizei uma visita simulada a uma padaria, onde os alunos vivenciaram a compra de Lanche, Queijo, Refrigerante e Bombom. Após isso, buscou-se alcançar os seguintes objetivos:

Interação: é o reconhecimento se o problema escolhido pode se transformar em uma aprendizagem significativa com o mundo real. Entre Situação real; modelagem; modelo e matemática.

Matematização:  é o reconhecimento da situação do problema, ou seja, visitar a padaria comprar: lanche, queijo, refrigerante e bombom, mostrando para o aluno que a modelagem matemática está na direção de um experiência prática.

Modelo matemático: é a Interpretação da solução, ou seja, com os dados propostos no problema devemos buscar uma solução concreta;

Formulação do problema: é criar hipóteses de que esta formulação seja capaz de modelar, obter uma resolução e validação.

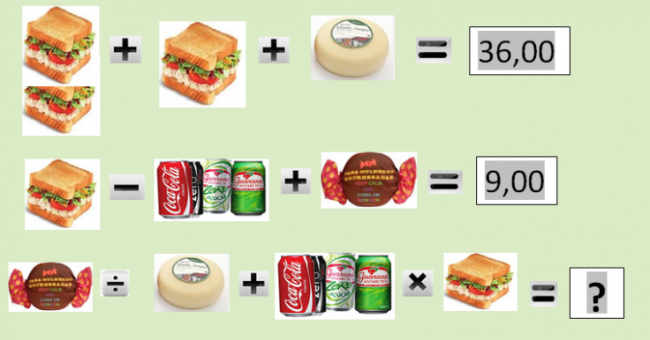
Conforme problema abaixo.

ensino de matemática, a dificuldade na aprendizagem está embutida ao rigor de abstração que esses conteúdos exigem, juntamente o modo que é ensinada, os conteúdos são trabalhados nas escolas, de maneira teórica, abrindo uma lacuna de difícil compreensão e aprendizagem dos alunos fazendo com que não reconheçam a importância da matemática em nosso dia a dia.

O desenvolvimento dos alunos envolvidos baseia-se, essencialmente, na modelagem matemática como metodologia. Inicialmente, professor e os alunos estudaram o processo de modelagem, suas etapas, características e exemplos de aplicações. De modo geral, na modelagem matemática, após a definição do tema, procede-se a coleta de dados. Quando não se tem um problema a priori, a investigação sobre o tema possibilita que seja identificado e definido um problema a ser abordado. Na fase denominada abstração, as hipóteses são formuladas, e assumidas as simplificações que fundamentam a elaboração do modelo matemático.

Dentre as diversas possibilidades que se apresentam no amplo e abrangente quando se trata de modelagem, inúmeros temas podem ser escolhidos, no nosso caso optamos pela visita simulada em uma padaria. Como a principal proposta do era elaborar modelos matemáticos para o ensino de equação de 1º grau, trabalhando expressões álgebras e seus elementos de ordem na Multiplicação, Divisão, Audição e Subtração, visando à contextualização de conteúdos e uma aprendizagem mais significativa. O principal objetivo na construção de diferentes modelos foi enfatizar a flexibilidade da modelagem matemática como estratégia de ensino de equações de 1º grau com a utilização de objetos ilustrativos, viabilizando a modificação de modelos por meio da incorporação de novas hipóteses.

Os dados utilizados foram a compra dos seguintes objetos na padaria: Lanche, Queijo, Refrigerante e Bombom.  Apresentam o modelo de Modelagem Matemática abaixo, no qual matemática e realidade são dois conjuntos disjuntos e a modelagem é o meio de fazê-los interagir.

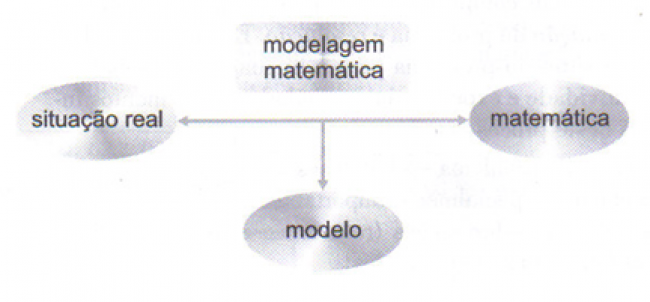
Essa interação, que permite representar um fenômeno através da linguagem matemática (modelo matemático), envolve uma série de procedimentos, que podem ser agrupados em três etapas, subdivididas em seis subetapas, a saber:

Interação

1.      

·         Reconhecimento da situação-problema;

·         Familiarização com o assunto a ser modelado    referencial teórico.

2.     Matematização

·         Formulação do problema hipóteses;

·         Resolução do problema em termos do modelo;

3.     Modelo matemático

·         Interpretação da solução;

·         Validação do modelo avaliação. 

Se o modelo não atender às necessidades que o geraram, o processo deve ser retomado na segunda etapa – Matematização – mudando-se ou ajustando hipóteses, variáveis, etc.

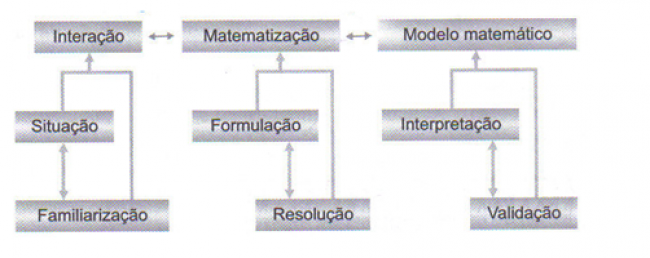
Com base no nosso caso que se trata de uma visita em uma padaria, com o intuito de trabalhar equação de 1º grau, expressão álgebra e expressões numéricas com utilização de objetos ilustrativos. Explicarei como trazemos a matemática na teoria abstrata para a vida prática. Interação: é o reconhecimento se o problema escolhido pode se transformar em uma aprendizagem significativa com o mundo real.

Matematização:  é o reconhecimento da situação problema, ou seja, visitar a padaria comprar: lanche, queijo, refrigerante e bombom, mostrando para o aluno que a modelagem na direção de um modelo.

Familiarização:

Modelo matemático: é a Interpretação da solução, ou seja, com os dados propostos no problema deve-se haver uma interpretação e achar a solução concreta;

Situação: é a modelagem matemática abstrata e precisamos transformar em um modelos matemáticos válidos.

Formulação do problema: é criar hipóteses de que esta formulação seja capaz de modelar, obter uma resolução e validação. 

A seguir darei a resolução do nosso problema proposto de modelagem matemática com a utilização de objetos ilustrativos no ensino e aprendizagem de equação de 1º grau e expressões numéricas.

Segunda linha: o aluno começou a vivenciar os elementos de ordens aplicados nas expressões numéricas, primeiro iniciamos pela soma, e depois a subtração. 1x – 4x + 1x = 9,00. Resolvemos temos: 2 + 16 – 9 =  9  Terceira linha: 1x +1x + 4x  X 1x  Resolvemos essa equação também, aplicando os elementos das expressões numéricas. Resolvendo de forma invertida. Neste caso como já sabemos o valor de cada item, basta aplicar para chegar o resultado. Então temos: 9 x 16 / 2 + 9 =  81

Para resolvemos expressões numéricas devemos saber essa sigla, (MDSS) primeiro resolvermos a Multiplicação, segundo a Divisão, terceiro a Soma e quarto a Subtração, conhecido como elemento das expressões numéricas. 

Valdivino Sousa

Professor, Matemático, Contador, Bacharel em Direito e Escritor.  

Pesquisador sobre Engenharia Didática em Matemática; Modelagem; Construção do Conhecimento em Matemática; 

Modelos Matemáticos e suas Aplicações.  Site: http://www.valdivinosousa.mat.br

Linhas(s) de Pesquisa / Área de Interesse: Engenharia Didática em Matemática; Modelagem; Construção do Conhecimento em Matemática; Modelos Matemáticos e suas Aplicações.  

REFERÊNCIAS BIBLIOGRÁFICAS 

BASSANEZI, Rodney Carlos. Ensino-aprendizagem com Modelagem Matemática. São Paulo: Ed. Contexto, 2004. 389 páginas.

BIEMBENGUT, Maria Sallet; HEIN, Nelson. Modelagem Matemática no Ensino. São Paulo: Editora Contexto, 2005. 127 páginas.

LIBANEO, José Carlos. Didática. São Paulo: CORTEZ, 1994. (Coleção Magistério 2° grau. Série Formação do Professor). 261 páginas.

PAIN, Sara. A Função da Ignorância. Trad. De Alceu Edir Fullaman. Porto alegre: Artes Medicas, 1987. 261 páginas.

TOLEDO, Marilia; TOLEDO, Mauro. Didática de Matemática: como dois e dois. São Paulo: FTD, 1997. 335 páginas.